Algoritmos Computacionais: Estruturas de decisão e repetição

Algoritmos computacionais são uma sequência de instruções (passos) que resolve um problema computacional.

Voltamos aos algoritmos não computacionais para aprendermos alguns conceitos importantes, na figura abaixo é descrito um algoritmo para utilizar um telefone público:

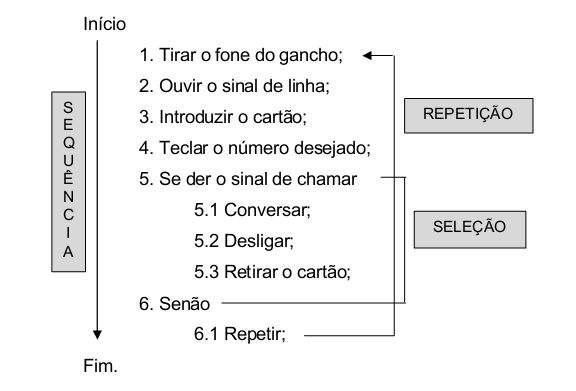Podemos definir como formas básicas para definir uma solução de qualquer problema as etapas de: Seqüência, Repetição e Seleção.

Naturalmente que os algoritmos para problemas resolvidos com o auxílio de computadores (algoritmos computacionais) não serão tão simples como os exemplos mostrados. Na figura abaixo dá uma idéia da utilidade dos Algoritmos.

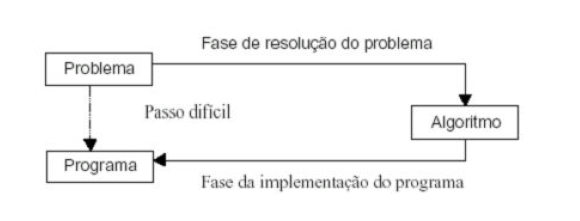Porque estudar algoritmos computacionais?

• Programar é basicamente construir algoritmos!
• O algoritmo é a fase que antecede a construção de um programa de computador!
• Aprender a programar é mais fácil quando sabemos algoritmos!

Forma de Representar Algoritmos

Existem diversas formas de representação de algoritmos, mas não há um consenso com relação à melhor delas.
As formas de representação de algoritmos mais conhecidas:

• Descrição Narrativa
• Fluxograma
• Pseudocódigo

Descrição Narrativa

Nesta forma de representação os algoritmos são expressos diretamente em linguagem natural. Exemplo:

Cálculo da média de um aluno:

1. Obter as notas da primeira e da segunda prova
2. Calcular a média aritmética entre as duas notas
3. Se a média for maior ou igual a 7
   3.1 O aluno foi aprovado
4. Senão
   4.1 O aluno foi reprovado

A representação narrativa é pouco usada na prática porque o uso de linguagem natural muitas vezes dá oportunidade a más interpretações, ambiguidades e imprecisões.

Fluxograma

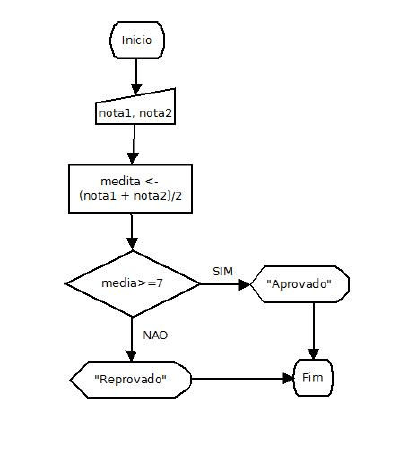
É uma representação gráfica de algoritmos onde formas geométricas diferentes implicamações (instruções, comandos) distintos. Tal propriedade facilita o entendimento das idéias contidas nos algoritmo. Exemplo:

Cálculo da média de um aluno:

Pseudocódigo

Esta forma de representação de algoritmos, também conhecida como português estruturado ou portugol, é bastante rica em detalhes e, por assemelhar-se bastante à forma em que os programas são escritos utilizando uma linguagem de programação, encontra muita aceitação, sendo portanto a forma de representação de algoritmos que será adotada nesta disciplina.

Muitas vezes esta representação é suficientemente geral para permitir que seja realizada uma tradução de um algoritmo utilizando pseudocódigo para uma linguagem de programação.

Exemplo, cálculo da média de um aluno:

Algoritmo Media
Var
nota1, nota2, media
Inicio
Leia(nota1, nota2)
media <- (nota1+nota2)/2 Se media >= 7 então
Escreva “Aprovado”
Senão
Escreva “Reprovado”
Fim Senão
Fim

Anatomia do algoritmo na forma de pseudocódigo

A estrutura básica do pseudocódigo é a seguinte:

Algoritmo <nome_do_algoritmo>
Var
   <declaração_de_variáveis>
Início
   <corpo_do_algoritmo>
Fim

Cada elemento tem um significado:

• Algoritmo é uma palavra que indica o início da definição de um algoritmo em forma de pseudocódigo.
• Nome algoritmo é um nome simbólico dado ao algoritmo com a finalidade de distingui-lo dos demais.
• Declaração de variáveis consiste em uma porção opcional onde são declaradas as variáveis globais usadas no algoritmo.
• Inicio e Fim são as palavras que delimitam o início e o término do conjunto de instruções do corpo do algoritmo.

Técnicas para elaboração de algoritmos computacionais

computador, a princípio, não executa nada. Para que ele faça uma determinada tarefa como calcular uma folha de pagamento, por exemplo, é necessário que ele execute um programa. Um programa é um conjunto de milhares de instruções que indicam ao computador, passo a passo, o que ele tem que fazer. Logo, um programa nada mais é do que um algoritmo computacional descrito em uma linguagem de programação. Uma linguagem de programação contém os comandos que fazem o computador escrever algo na tela, realizar cálculos aritméticos, receber uma entrada de dados via teclado, e milhares de outras coisas, mas estes comandos precisam estar em uma ordem lógica.

O termo processamento de dados é muitas vezes utilizado em conjunto com computadores, pois, em geral, é isto o que eles fazem: processar dados. Daí podem extrair os dois componentes básicos de um algoritmo computacional: Dados são os valores (números, nomes, etc.) de que precisamos para resolver o problema e Código são os comandos ou instruções que usaremos para manipular e “processar” os dados.

Variáveis

Uma variável, é um espaço da memória do computador que “reservamos” para guardar informações (dados). Como o próprio nome sugere, as variáveis, podem conter valores diferentes a cada instante de tempo, ou seja, seu conteúdo pode variar de acordo com as instruções do algoritmo. Os dados que um algoritmo trabalha são armazenados em variáveis, essas informações são guardadas temporariamente até o termino da execução do algoritmo.

As variáveis são referenciadas através de um nome (identificador) criado por você durante o desenvolvimento do algoritmo. Exemplos de nomes de variáveis: produto, idade, a, x, nota1, peso, preço, etc. O conteúdo de uma variável pode ser alterado, consultado ou apagado quantas vezes forem necessárias durante o algoritmo. Mas, ao alterar o conteúdo da variável, a informação anterior é perdida, ou seja, sempre “vale” a última informação armazenada na variável. Uma variável armazena ‘apenas’ um conteúdo de cada vez.

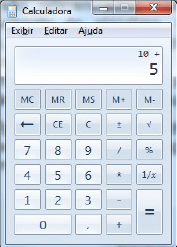
Exemplo: Na figura abaixo podemos observar a calculadora do Windows, imagine que necessitamos efetuar uma simples operação de soma (10+5). Tanto os valores de entrada (5 e 10) quando o resultado da adição (15) são armazenados em variáveis, isso é uma prática comum em qualquer programa de computador que necessite executar algum processamento e mostrar um resultado do mesmo.

Tipos de Dados

Para manter a integridade dos dados, toda variável deve ser classificada de acordo com o tipo de valor a ser armazenado.

Tipo	Descrição
INTEIRO	Representa valores inteiros Exemplos: 10, 5, -5, -10
REAL	Representa valores reais (com ponto separador da parte decimal). Exemplos: 10, 15.5, -14.67
CARACTERE	Representa texto (seqüência de caracteres) em aspas duplas. Exemplos: “João Novaes”, “B”, “123456”, “66.110-054”
LOGICO	Representa valores lógicos. Exemplo: verdadeiro ou falso

Declaração de variáveis

Declarar uma variável consiste na definição dos nomes e dos tipos para as variáveis que serão utilizadas pelos algoritmos, antes de sua utilização. O significado da declaração de variáveis corresponde à criação de locais na memória rotulada com o nome da variável (identificador) e marcada com o tipo de valores que ela pode conter. Como podemos observar na ilustração:

O significado da declaração de variáveis corresponde à criação de locais na memória rotulada com o nome da variável (identificador) e marcada com o tipo de valores que ela pode conter isso é necessário para que os programas manipulem valores e executem tarefas.

Para que os programas manipulem valores, estes devem ser armazenados em variáveis e para isso, devemos declará-las de acordo com a sintaxe:

var
<nome_da_variável>: <tipo_da_variável>
ou
var
<nome_da_variável_1>, <nome_da_variável_2>: <tipo_da_variável>
Exemplo:
var
nome: caractere
salario: real
idade: inteiro
tem_filhos: logico

• A palavra-reservada VAR deverá estar presente sempre e será utilizada um única vez na definição de um conjunto de uma ou mais variáveis;
• Numa mesma linha poderão ser definidas uma ou mais variáveis do mesmo tipo; Para tal, deve-se separar os nomes das mesmas por vírgulas;
• Variáveis de tipos diferentes devem ser declaradas em linhas diferentes.

Regras para definição de variáveis

• Nomes de variáveis não podem ser iguais a palavras reservadas;
• Nomes de variáveis devem possuir como primeiro caractere uma letra;
• Não utilizar caracteres especiais, exceto o “_” (underscore ou sublinhado);
• Ser sucinto e coerente;
• Nomes de variáveis não podem conter espaços em branco;
• Na sintaxe do Português Estruturado, não há diferença entre letras maiúsculas de minúsculas.

Palavras reservadas

Palavra reservada ou palavra chave, são termos que tem um uso específico para a linguagem, não podem ser usadas como identificadores e possuem esse nome pois são reservadas para uso da gramática da linguagem.

Exemplos: algoritmo, var, inicio, fimalgoritimo, se, para, enquanto, verdadeiro, falso, etc.

Operadores, Atribuição

Na grande maioria dos problemas, para sua solução, é necessário que as variáveis tenham seus valores consultados ou alterados e, para isto, devemos utilizar um conjunto de operadores.

Operador de atribuição

Para atribuir ou “colocar” um valor em uma variável durante um algoritmo, utilizamos o operador de atribuição. O operador de atribuição é representado por uma seta (<-) apontando para a esquerda.

Exemplo:

nome <- “Brayan Santos”
salario <- 2500.67
idade <- 10
tem_filhos <- FALSO

Operadores aritméticos

Ao desenvolvermos algoritmos, é comum utilizarmos expressões matemáticas para a resolução de cálculos. Os operadores aritméticos disponíveis são:

Operador	Representação	Exemplo
Adição	+	R <- 10 + 5
Subtração	–	R <- 10 – 5
Multiplicação	*	R <- 10 * 5
Divisão	/	R <- 10 / 5
Exponenciação	^	R <- 10 ^ 5
Módulo da divisão	mod	R <- 10 mod 5

Linearização (horizontalização) de Expressões: Para a construção de algoritmos que realizam cálculo matemáticos, todas as expressões aritméticas devem ser linearizadas, ou seja, colocadas em linhas.

• Forma tradicional:

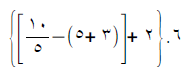• Computacional: ((10/5-(5+3))+2)*6

Operadores relacionais

São utilizados para estabelecer uma relação de comparação entre variáveis ou expressões. O resultado dessa comparação sempre será um valor lógico (Verdadeiro ou Falso).

Operador	Representação	Exemplo
Maior	>	A > B
Menor	<	A < B
Maior ou igual	>=	A >= B
Menor ou igual	<=	A <= B
Igual	=	A = B
Diferente	<>	A <> B

Comparações só podem ser feitas entre objetos de mesma natureza, isto é variáveis do mesmo tipo de dado.

Operadores lógicos

Os operadores lógicos servem para combinar resultados de expressões, retornando se o resultado final é verdadeiro ou falso.

Operador	Representação	Exemplo	Significado
Conjunção	e	A e B	Resulta VERDADEIRO se ambas as partes forem verdadeiras.
Disjunção	ou	A ou B	Resulta VERDADEIRO se uma das partes é verdadeira.
Negação	não	nao A = B	Nega uma afirmação, invertendo o seu valor lógico: se for VERDADEIRO torna-se FALSO, se for FALSO torna-se VERDADEIRO.

A tabela abaixo é chamada de tabela verdade, ela mostra os resultados das aplicações dos operadores lógicos conforme os valores dos operadores envolvidos.

A	B	A e B	A ou B	nao A
verdadeiro	verdadeiro	verdadeiro	verdadeiro	falso
verdadeiro	falso	falso	verdadeiro	falso
falso	verdadeiro	falso	verdadeiro	verdadeiro
falso	falso	falso	falso	verdadeiro

De acordo com a necessidade, as expressões podem ser unidas pelos operadores lógicos.
Exemplo: (2+5>4) e (3<>3) resulta FALSO, pois VERDADEIRO e FALSO resulta FALSO.

A modularização é a divisão de uma expressão em partes menores, facilitando assim o entendimento e definindo prioridades para a resolução da mesma. No exemplo anterior notamos que, em expressões computacionais utilizamos somente parênteses “()” para modularização. Na sintaxe do Português Estruturado podemos ter parênteses dentro de parênteses, como seriam os colchetes e as chaves na matemática.

Os parênteses indicam quais sub-expressões, dentro de uma expressão, serão executados primeiro. A princípio, a execução é da esquerda para direita, mas além dos parênteses, existem prioridades entre os operadores envolvidos na expressão. Tais prioridades são mostradas nas tabelas:

Operador Aritmético	Prioridade
Exponenciação	3
Multiplicação	2
Divisão	2
Adição	1
Subtração	1

Exemplo:

• (2 + 2)/2 resulta 2
• 2 + 2/2 resulta 3

Operador Lógico	Prioridade
e	3
ou	2
não	1

Exemplo:

• (2>3) ou (3<2) e (2<3) o resultado seria Falso
• (2>3) e (3<2) ou (2<3) o resultado seria Verdadeiro

Entre as categorias de operadores também há prioridades, conforme mostrado na tabela abaixo.

Operador	Prioridade
Operadores aritméticos	3
Operadores relacionais	2
Operadores lógicos	1

A maioria das linguagens de programação não possui relacionamento de categorias.
2*5>3 ou 5+1<2 e 2<7-2 // resulta em erro.

(2*5>3) ou (5+1<2) e (2<7-2) // forma correta

Comando entrada e saída

Em geral, um programa que não lê dados para realizar um processamento e não tem como mostrar seus resultados é inútil. Portanto, em algum ponto de todo algoritmo deve ocorrer a leitura e a exibição de valores, e todas as linguagens de programação têm comandos para este fim.

Leitura

Para que o algoritmo possa obter dados do mundo exterior para processamento, estes devem vir através de dispositivos de entrada (normalmente teclado). Em Português estruturado usamos o comando Leia, a sintaxe do comando é:

Leia(<identificador>)
Exemplo:
Leia(nome)

Escrita

Para que os algoritmos possam apresentar ao usuário os resultados do processamento dos dados para processamento, que normalmente é utilizado o monitor de vídeo, usamos o comando Escreva, a sintaxe do comando é:

Escreva(<identificador>)
Escreva(“<expressão>”)
Escreva(“<expressão>”,<identificador>)
Exemplo:
Escreva(nome)
Escreva(“Você foi aprovado”)
Escreva(“Média do aluno: ”,media)

Os comandos de Leia e Escreva são utilizados em conjunto durante a construção do algoritmo. Veja no exemplo um algoritmo completo que faz a leitura de dois valores inteiros, faz a adição entre eles e exibe o resultado ao usuário.
Exemplo:

Algoritmo Soma
Var
n1, n2, resultado: inteiro
Inicio
Leia(n1)
Leia(n2)
resultado <- n1 + n2
Escreva(resultado)
FimAlgoritmo

Estruturas de decisão

Até o momento os algoritmos estudados utilizam apenas instruções primitivas de atribuição, e de entrada e saída de dados. Qualquer conjunto de dados fornecido a um algoritmo as instruções serão executadas sempre na mesma sequência.

Mas na prática muitas vezes é necessário executar ações diversas em função dos dados fornecidos ao algoritmo. Em outras palavras, dependendo do conjunto de dados de entrada do algoritmo, deve-se executar um conjunto diferente de instruções.

Também conhecida como estrutura de seleção, permite que determinadas instruções sejam executadas ou não, dependendo do resultado de uma condição (teste), ou seja, o algoritmo vai ter mais de uma saída, uma opção que será executada de acordo com o teste realizado.

Leia também: Informática Básica: hardware e software

Estruturas de decisão simples

Nesta estrutura uma única condição (expressão lógica) é avaliada. Dependendo do resultado desta avaliação, um comando ou conjunto de comandos serão executados (se a avaliação for verdadeira) ou não serão executados (se a avaliação for falsa).

Sintaxe:
Se (<condição>) entao
<instruções se a condição for verdadeira>
fimse
Exemplo: Verificar se um valor inteiro fornecido pelo usuário é positivo
algoritmo TestaPositivo
var
numero: inteiro
inicio
leia (numero)
se (numero > 0) entao
Escreva ("O numero é positivo")
fimse
fimalgoritmo

Observe que a mensagem “O numero é positivo” só será exibida SE o resultado da expressão “numero >0” retornar VERDAERIO. Outro detalhe importante é que o termo “<condição>” só deve possuir expressões que retornem um valor lógico: VERDADEIRO ou FALSO.

Exemplo:
se(media>7)
se((A>B)e(A>C))
se(senha="123456")

Estruturas de decisão composta

Nesta estrutura se executa um comando (ou sequência de comando) se uma condição é verdadeira, e se executa um outro comando (ou sequência de comandos) se a condição é falsa.

Sintaxe:
Se (<condição>) então
<instruções se a condição for verdadeira>
Senao
<instruções se a condição for falsa>
fimse
Exemplo: Verificar se um valor inteiro fornecido pelo usuário é par ou impar.
algoritmo TestaParImpar
var
numero: inteiro
inicio
escreva ("Informe o numero")
leia (numero)
se (numero mod 2 = 0) então
escreva ("O numero é par")
senao
escreva ("O numero é impar")
fimse
fimalgoritmo

Somente um bloco será executado, nunca ambos.

Estruturas de decisão aninhada ou encadeada

A estrutura também permite o aninhamento, ou seja, o comando a ser executado dentro de uma seleção (“Se” ou “Senão”) pode ser uma outra seleção, não tendo limite para o número de seleções dentro de uma seleção. Nos casos de vários aninhamentos subsequentes, uma boa indentação será fundamental para um bom entendimento de do pseudocódigo.

Sintaxe:
se (<condição_1>) entao
<instruções para condição1 verdadeira>
senao
se(<condição_2>) entao
<instruções para condição2 verdadeira, porém condição1 falsa>
senao
<instruções para condição1 e condição2 falsas>
fimse
fimse

Exemplo: Efetuar o cálculo do reajuste de salário de um funcionário. Considere que o funcionário deve receber um reajuste de 15% caso seu salário seja menor que 500. Se o salário for maior ou igual a 500, mas menor ou igual a 1000, seu reajuste será de 10%; caso seja ainda maior que 1000, o reajuste deve ser de 5%. Ao final o algoritmo deve apresentar o valor do novo salário.

Observe que, para resolver o problema apresentado, é necessário utilizar uma de três condições para calcular o reajuste do salário do funcionário, sendo:

• Salário <500, reajuste será de 15%
• Salário >= 500, mas <= 1000, reajuste será de 10%
• Salário > 1000, reajuste será de 5%

As condições em questão devem ser encadeadas, pois todas as possibilidades de reajuste devem ser cercadas.

Algoritmo ReajusteSalario
var
novo_salario, salario: real
inicio
escreva ("Informe o salario")
leia (salario)
se (salario < 500) entao
novo_salario <- salario * 1.15
senao
se (salario <= 1000) entao
novo_salario <- salario * 1.10
senao
novo_salario <- salario * 1.05
fimse
fimse
escreva (novo_salario)
fimalgoritmo

Estruturas de Repetição

No ponto que atingimos de nosso estudo sempre foi possível resolver os problemas propostos com algoritmos em uma sequencia linear de operações. Observe o exemplo que segue, ele faz a leitura do nome, de duas notas e exibe a média para 4 alunos aluno:

Exemplo:
algoritmo "MediaAlunos"
var
nome: caractere
nota1, nota2, media: real
inicio
leia(nome)
leia(nota1)
leia(nota2)
media <- (nota1+nota2)/2
escreval("Nome: ",nome, " Media: ",media)
leia(nome)
leia(nota1)
leia(nota2)
media <- (nota1+nota2)/2
escreval("Nome: ",nome, " Media: ",media)
leia(nome)
leia(nota1)
leia(nota2)
media <- (nota1+nota2)/2
escreval("Nome: ",nome, " Media: ",media)
leia(nome)
leia(nota1)
leia(nota2)
media <- (nota1+nota2)/2
escreval("Nome:

A solução no exemplo é viável apenas para situações onde temos uma turma de poucos alunos; para uma turma de 80 alunos, a implementação da solução seria muito trabalhosa. É para problemas como esse que temos um conjunto de estruturas sintáticas que permitem que um trecho de um algoritmo seja repetido um determinado número de vezes, sem que o código correspondente tenha que ser escrito por várias vezes.

Estrutura de repetição: enquanto…faca

Na estrutura enquanto..faca, um teste lógico é realizado no início de um laço, se o resultado for verdadeiro uma lista de comandos é executada. Isso é repetido até que a condição seja falsa.

Sintaxe:
Enquanto (<condição>) faca
<listas de comandos>
FimEnquanto
Exemplo: Fazer a leitura sucessiva de 2 notas notas e apresentar a média de 4 alunos
algoritmo "MediaAlunosRepeticao"
var
nome: caractere
nota1, nota2, media: real
cont: inteiro
inicio
cont <- 1
enquanto (cont <=4) faca
leia(nome)
leia(nota1)
leia(nota2)
media <- (nota1+nota2)/2
escreval("Nome: ",nome, " Media: ",media)
cont <- cont + 1
fimenquanto
fimalgoritmo

Observação: A variável cont é inicializada com o valor 1 (um) antes do inicio da repetição; e a cada vez que o laço for realizado o valor dela será acrescida de 1 (um). Isso torna possível o controle de quantas vezes a estrutura será repetida e evita que o laço fique se repetindo indefinidamente (laço infinito).

Existem diversas maneiras de implementar o mesmo laço, mas todo laço com variável de controle deve conter:

• Inicialização da variável de controle;
• Incremento (aumento do valor da variável de controle) ou decremento (diminuição do valor da variável de controle) da variável de controle; e
• Teste de valor da variável de controle.

Exemplo: Escrever os números entre 1 e 100
algoritmo "Numeros"
var
cont: inteiro
inicio
cont <- 1
enquanto (cont <=100) faca
escreval(cont)
cont <- cont + 1
fimenquanto
fimalgoritmo
Exemplo: Escrever os números pares entre 1 e 100
algoritmo "NumerosPares"
var
cont: inteiro
inicio
cont <- 1
enquanto (cont <=100) faca
se(cont mod 2 = 0) entao
escreval(cont)
fimse
cont <- cont + 1
fimenquanto
fimalgoritmo

Estrutura de repetição: repita…ate

Na estrutura repita…ate, uma lista de comandos é executada e somente após isso uma condição é testada. Isso é repetido até que a condição seja falsa.

Sintaxe:

repita
<listas de comandos>
ate(<condição>)

Exemplo: Escrever os números pares entre 1 e 100

algoritmo "NumerosRepita"
var
cont: inteiro
inicio
cont <- 1
repita
escreval(cont)
cont <- cont + 1
ate (cont = 101)
fimalgoritmo

Observação: A estrutura repita…ate também é uma estrutura de repetição, semelhante à enquanto…faca. A diferença básica entre as duas estruturas é a posição onde é testada a condição. Na estrutura repita, a condição é avaliada após a execução dos comandos, o que garante que os comandos serão executados pelo menos uma vez.

Na estrutura enquanto, a expressão é avaliada no início e se o resultado for FALSO no primeiro teste, a lista de comandos não é executada nenhuma vez. Essa diferença faz com que em determinadas situações o uso de uma estrutura seja mais vantajoso que o uso da outra.

Estrutura de repetição: para,faca

Na estrutura para..faca, a variável de controle é inicializada com e no início de cada iteração, seu valor é comparado com . Se o valor da variável for menor ou igual a , a lista de comandos é executada e após ser executado o último comando da lista, a variável de controle é incrementada. Isto repete-se até que o valor da variável de controle seja maior que , quando então é executado o comando imediatamente após a palavra fimpara.

Sintaxe:
para<variável de controle> de<valor inicial> ate<valor final> [passo
<incremento>] faca
<lista de comandos>
fimpara
Exemplo: Escrever os números pares entre 1 e 100
algoritmo "NumerosPara"
var
i: inteiro
inicio
para i de 1 ate 100 passo 1 faca
escreval(i)
fimpara
fimalgoritmo

A diferença entre estrutura de repetição para..faca e as outras vistas anteriormente é que ela é uma estrutura mais completa que as anteriores, pois ela incorpora a inicialização, incremento e teste de valor final da variável de controle. É preferencialmente utilizada em situações em que sabe-se previamente o número de repetições a serem feitas.

Conclusão

O artigo ficou bem completo no assunto que nos propomos a falar nesse artigo, façam bom proveito desse material, compartilhem com os colegas de vocês da faculdade.